Nonlinear finite elements/Nonlinearities in solid mechanics
Nonlinearity is natural in physical problems. In fact the linear assumptions we make are only valid in special circumstances and usually involve some measure of "smallness", for example, small strains, small displacements, small rotations, small changes in temperature, and so on.
We use linear approximations not because they are more correct but because
- Linear solutions are easier to compute.
- The computational cost is smaller.
- Solutions can be superposed on each other.
However, linear analysis is not adequate and nonlinear analysis is necessary when
- Designing high performance components.
- Establishing the causes of failure.
- Simulating true material behavior.
- Trying to gain a better understanding of physical phenomena.
The choice of analysis depends on the problem at hand. The usual questions an engineer asks when deciding on the type of analysis to perform are
- What is the goal of the analysis?
- What are the acceptable amounts of error?
A cost-benefit analysis is usually necessary before embarking on the nonlinear analysis of a problem.
Types of Nonlinearity[edit]
Nonlinearities are classified into two major types:
- Geometric nonlinearities.
- Material nonlinearities.
Geometric nonlinearities[edit]
Geometric nonlinearities involve nonlinearities in kinematic quantities such as the strain-displacement relations in solids. Such nonlinearities can occur due to large displacements, large strains, large rotations, and so on. Contact can also be classified as a geometric nonlinearity because the area of contact is a function of the deformation (some authors puts contact in another class called nonlinear boundary conditions).
An example of a problem that involves a geometric nonlinearity is the torsional spring problem (see Figure 1).
We want to find the relationship between the rotation θ of the bar and the applied force F.
A balance of moments on the bar gives us
where M is the moment at the pinned end of the bar.
We can relate the moment M to the rotation of the spring by the constitutive equation for a torsional spring
where kT is the torsional spring constant.
Therefore, we can write
If the angular displacement θ is small (i.e.,  ), we have
), we have  . Therefore, the force-rotation relationship becomes
. Therefore, the force-rotation relationship becomes
 ), we have
), we have  . Therefore, the force-rotation relationship becomes
. Therefore, the force-rotation relationship becomes
Figure 2 shows how the linear approximation compares with the nonlinear solution. The nonlinear and linear solutions are quite different beyond a rotation of around 30 degrees.
Material nonlinearities[edit]
Material nonlinearities occur when the stress-strain or force-displacement law is not linear, or when material properties change with the applied loads.
For the torsional spring, we can introduce material nonlinearities if we assume that the constitutive equation for the spring is
In that case, the force-rotation relation becomes
If we assume small rotations, we get
Figure 3 shows how the inclusion of material nonlinearities affects the solution.
Nonlinier adalah wajar dalam masalah fisik. Bahkan asumsi linier kita buat ini hanya berlaku dalam keadaan khusus dan biasanya melibatkan beberapa ukuran "kekecilan", misalnya, strain kecil, perpindahan kecil, rotasi kecil, perubahan kecil suhu, dan sebagainya.
Kami menggunakan pendekatan linier bukan karena mereka lebih benar tetapi karena
- Solusi linier lebih mudah untuk menghitung.
- Biaya komputasi lebih kecil.
- Solusi dapat disuperposisikan satu sama lain.
Namun, analisis linier tidak memadai dan analisis nonlinier diperlukan ketika
- Merancang komponen kinerja tinggi.
- Menetapkan penyebab kegagalan.
- Simulasi perilaku material benar.
- Mencoba untuk lebih memahami fenomena fisik.
Pemilihan analisis tergantung pada masalah yang dihadapi. Pertanyaan-pertanyaan biasa seorang insinyur bertanya ketika memutuskan pada jenis analisis untuk melakukan yang
- Apa tujuan dari analisis?
- Apakah jumlah yang diterima dari kesalahan?
Sebuah analisis biaya-manfaat biasanya diperlukan sebelum memulai analisis nonlinier masalah.
Jenis Nonlinieritas[ sunting ]
Nonlinier diklasifikasikan menjadi dua jenis utama:
- Nonlinier geometrik.
- Bahan nonlinier.
nonlinier geometrik[ sunting ]
Nonlinieritas geometri melibatkan nonlinier dalam jumlah kinematik seperti strain-perpindahan hubungan dalam padatan. Nonlinier tersebut dapat terjadi karena perpindahan yang besar, strain besar, rotasi besar, dan sebagainya. Kontak juga dapat diklasifikasikan sebagai nonlinier geometrik karena bidang kontak adalah fungsi dari deformasi (beberapa penulis menempatkan kontak di kelas lain yang disebut kondisi batas nonlinier).
Contoh masalah yang melibatkan nonlinier geometrik adalah masalah pegas torsi (lihat Gambar 1).
Kami ingin mencari hubungan antara rotasi θ bar dan gaya F diterapkan.
Keseimbangan saat di bar memberi kita
dimana M adalah saat di akhir disematkan bar.
Kita dapat menghubungkan M saat ke saat rotasi musim semi dengan persamaan konstitutif untuk pegas torsi
di mana k T adalah konstanta pegas torsi.
Oleh karena itu, kita dapat menulis
Jika perpindahan sudut θ kecil (yaitu,  ), Kita memiliki
), Kita memiliki  . Oleh karena itu, hubungan kekuatan-rotasi menjadi
. Oleh karena itu, hubungan kekuatan-rotasi menjadi
 ), Kita memiliki
), Kita memiliki  . Oleh karena itu, hubungan kekuatan-rotasi menjadi
. Oleh karena itu, hubungan kekuatan-rotasi menjadi
Gambar 2 menunjukkan bagaimana pendekatan linier membandingkan dengan solusi nonlinier. Solusi nonlinier dan linier sangat berbeda di luar rotasi sekitar 30 derajat.
Bahan nonlinier[ sunting ]
Bahan nonlinier terjadi ketika hukum tegangan-regangan atau kekuatan-perpindahan tidak linear, atau ketika sifat material berubah dengan beban diterapkan.
Untuk pegas torsi, kita dapat memperkenalkan nonlinier material jika kita mengasumsikan bahwa persamaan konstitutif untuk musim semi adalah
Dalam hal ini, hubungan kekuatan-rotasi menjadi
Jika kita mengasumsikan rotasi kecil, kita mendapatkan
Gambar 3 menunjukkan bagaimana masuknya nonlinier materi mempengaruhi solusi.
Kategori :

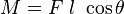


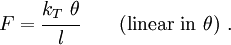



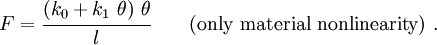

Tidak ada komentar:
Posting Komentar